THANK YOU FOR SUBSCRIBING
 Kathryn Zhao, Global Head of Electronic Trading, Wei Mao, Director FX Algorithmic Trading and Liang Liu, Head of Quant Research Electronic Trading, Cantor Fitzgerald
Kathryn Zhao, Global Head of Electronic Trading, Wei Mao, Director FX Algorithmic Trading and Liang Liu, Head of Quant Research Electronic Trading, Cantor FitzgeraldThe execution of an order with a relatively large size is always a non-trivial task. Generally speaking, itcan be done in two ways: sweep the market and get the order done at time zero; or split the order in small pieces and unwind the position in a prolonged time frame. The fast execution can achieve the execution with the smallest risk butwill inevitably create extensive market impact that leads to poor execution performance. Although FX market is highly fragmented, it is running as an ecosystem. The extensive market impact caused in one venue is spreading to the whole ecosystem with an ignorable delay. The slower execution avoids extensive market impact at the cost of increased uncertainty about the execution price. Liquidity seeking algorithm is trying to balance the risk and cost in an optimized fashion.
Methodology
Depending on a trader’s goal, this algorithm can be set up in two different manners: minimize the execution cost while satisfying the risk constraint; or minimize the risk while satisfying the cost constraint. In the following, we will discuss the first approach. Then understanding the second approach becomes straightforward.
The primary task of this algo is to find the optimal execution trajectory, namely size to execute along the time. If the time horizon is discretized into n slices, an execution trajectory is essentially a vector of order size on each time slice, X = (x1, x2, … xn-1, xn). Then it can be formulated as the following optimization problem
where C is the cost matrix and R is the risk matrix. This is a quadratic optimization with quadratic constraint.
The risk constraint is usually specified at the beginning of the trading and theabove formulation is well justified for initial optimization. As the execution progresses, the realized execution may deviate from the initial optimal trajectory. The market condition as well as the trader’s risk tolerance can also change. Therefore, it is necessary to re-optimize the execution trajectory. To treat the trader’s risk tolerance in a self-consistent fashion, we do the following optimization
where λ is the risk aversion coefficient,also the dual-valueof the initial optimization (1).
Market Impact Model
 In (1) and (2), the cost matrix C determines the execution cost created by the executiontrajectory X. Of all cost components, market impact isthe dominant one.
In (1) and (2), the cost matrix C determines the execution cost created by the executiontrajectory X. Of all cost components, market impact isthe dominant one.
Traditionally, people use proprietary internal trade records that accumulated over long history to derive the market impact model. There are two major drawbacks of this approach: the results are very noisy, and the R2 is generally very small; since the market changes all the time, using data with years’ age to estimate market impact of current trading is questionable. We have developed a proprietary methodology to estimate the market impact using most recent market data with great statistical significance.
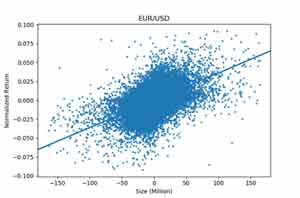
In our market impact modelling, the trade data was aggregated (buys minus sells) to get net trade flow over different time buckets. Then the regressions between the net trade flow and the associated market price return for different time horizonswere performed. The strong linear relationshipswere found. Figure 1 shows the regression result for 1-minute time horizon.
 Further research was done to explore how the regression result changes with the time horizon. We came to the conclusion that there is clearlydecaying nature of the market impact.The execution at a particular time can impact not only locally, but also later time in a decaying fashion. As a result, the following propagator formula is used to estimate the market impact from the execution at time s on a later time t
Further research was done to explore how the regression result changes with the time horizon. We came to the conclusion that there is clearlydecaying nature of the market impact.The execution at a particular time can impact not only locally, but also later time in a decaying fashion. As a result, the following propagator formula is used to estimate the market impact from the execution at time s on a later time t
where is the trading rate at time s, c is the impact coefficient, ϒis the decay power, and σis the volatility.With this formula, the items within the cost matrix can be calculated.
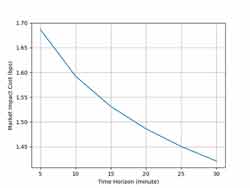
As we can see from formula (3), for a fixed order size, increasing the trading rate (reducing time horizon T) results in greater market impact cost. Taking a 100M EUR/USD order as an example, with the daily volatility as 0.01, if T changes from 5 minutes to 30 minutes, the market impact cost changes from 1.69bps to 1.42bps, as shown in Figure 2.
Risk Calculation
For an execution trajectory (x1, x2 …… xn) in time slices (Δ1, Δ2 …… Δn), the risk accumulated in the ith slice is

Risk accumulated in all slices is

From the above expression, we can derive the risk matrix in (1) and (2).
Examples
Liquidity seeking algorithm manages the trade-off between market impact and price risk. Traders may have different risk aversion as well as sensitivity to impact cost. The algorithm builds anoptimized execution trajectory based on the urgencyand maximum participation rate specified by the trader. Figure 3 shows two execution trajectories for a 100M EUR/USD order with two different urgency levels. The first one, with a higher urgency,is trading faster, especially at the beginning.The flat start is because of the maximum participation rate.

Liquidity seeking algorithm optimizes the execution trajectory based on the market conditions as well, such as market liquidity, volatility, etc. Figure 4 shows two execution trajectories for a 100M EUR/USD order at different hours. Both are on the same urgency level. The first one, at more liquid hour, is trading faster, especially at the beginning.

Read Also